Hierarchical Reasoning Model : Thinking fast and Slow
What if the next leap in AI isn’t bigger models, but models that know when to think longer? HRMs promise the same utopia, HRMs are one of the early step toward models that pause, plan, and budget.
Table of content
Introduction
But, how do we measure the quality of reasoning today?
How Modern day LLMs reason?
Token-level reasoning
Latent-level reasoning
The Ideal Case
Methodology : how HRM actually works?
Architecture breakdown
Why this avoids premature convergence?
Training : constant memory, DEQ-style math, and deep supervision
Halting / adaptive computation (ACT + Q-learning)
Losses, objectives, and what actually gets optimized
Inference pipeline
Complexity & resource tradeoffs
Annotated pseudo-code
How HRM relates to other recurrent improvements (xLSTM, hierarchical RNNs, DEQs)?
Results/Outcomes
Thoughts
Conclusion
Introduction
Reasoning has been our recurring theme for a while now. In earlier articles, we looked at why reasoning might emerge from optimization itself, and later at how architectures like CTMs push reasoning into the latent space. Each time, the takeaway was clear: reasoning isn’t just another “capability” bolted onto LLMs; it’s the very heartbeat of intelligence. Without it, models can generate fluent text but fail at the simplest logical test; with it, even a smaller model can surprise us with creative leaps.
That’s why this new paper caught my eye. It doesn’t just throw more data or parameters at the problem, it proposes a different way of definition of thought. Instead of treating reasoning as a token-by-token chain (like CoT), the authors introduce a Hierarchical Reasoning Model (HRM): a brain-inspired recurrent system where slow and fast processes interact, almost like conductor and orchestra.
Why is this relevant? Because if true reasoning requires more than scaling transformers, then HRM may be one of those architectural pivots we’ve been anticipating where models start thinking in latent structures, not just word sequences.
But, how do we measure the quality of reasoning today?
If we say a model “reasons well,” what do we actually mean? Unlike fluency or speed, reasoning isn’t obvious to measure. It hides in how models handle patterns, rules, and abstractions. Over the last few years, the community has converged on a few categories that help us pin down what reasoning quality looks like:
Patterned reasoning: puzzles like number sequences, Sudoku, or arithmetic word problems, where the challenge is spotting hidden regularities.
Logical reasoning: tasks involving if–then rules, symbolic manipulation, or multi-step deduction.
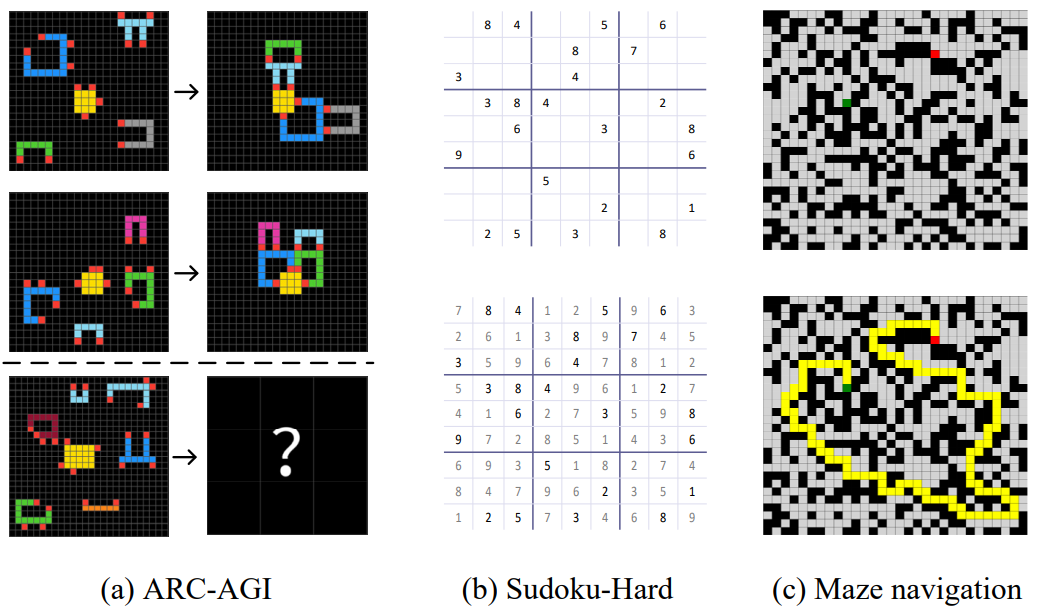
Abstract reasoning: problems like ARC-AGI (Abstraction and Reasoning Corpus), which test whether a model can discover structure from very few examples; sort of, reasoning in the wild.
Relational reasoning: mazes, graphs, and pathfinding problems where models must juggle spatial or structural relations rather than just language.
Each category brings out a different facet of reasoning. A model good at Sudoku might still fail on ARC-AGI, and one that can parse logic may still stumble on spatial mazes. That’s why benchmark suites matter; they act like prisms, splitting the broad notion of “reasoning” into testable beams. You can read about these benchmarks and many more in our article here : Benchmarks Article
This is where HRM positions itself. Instead of measuring success on language-heavy benchmarks, it dives straight into the hard reasoning benchmarks:
ARC-AGI, long considered one of the most difficult open tests of abstraction.
Sudoku-Extreme, which demands strict logical consistency.
Maze-Hard, where relational reasoning is everything.
What’s striking is that HRM isn’t just competing, here it’s doing so with a tiny 27M parameter model, no pre-training, and ~1,000 training samples. That combination makes the results even more relevant: if reasoning quality shows up under those conditions, it suggests that the architecture itself, not just scale plays a central role.
How Modern day LLMs reason?
When people talk about reasoning in today’s large language models, they usually mean one of two broad styles and both come with their own strengths, weaknesses, and growing pains.
Token-level reasoning
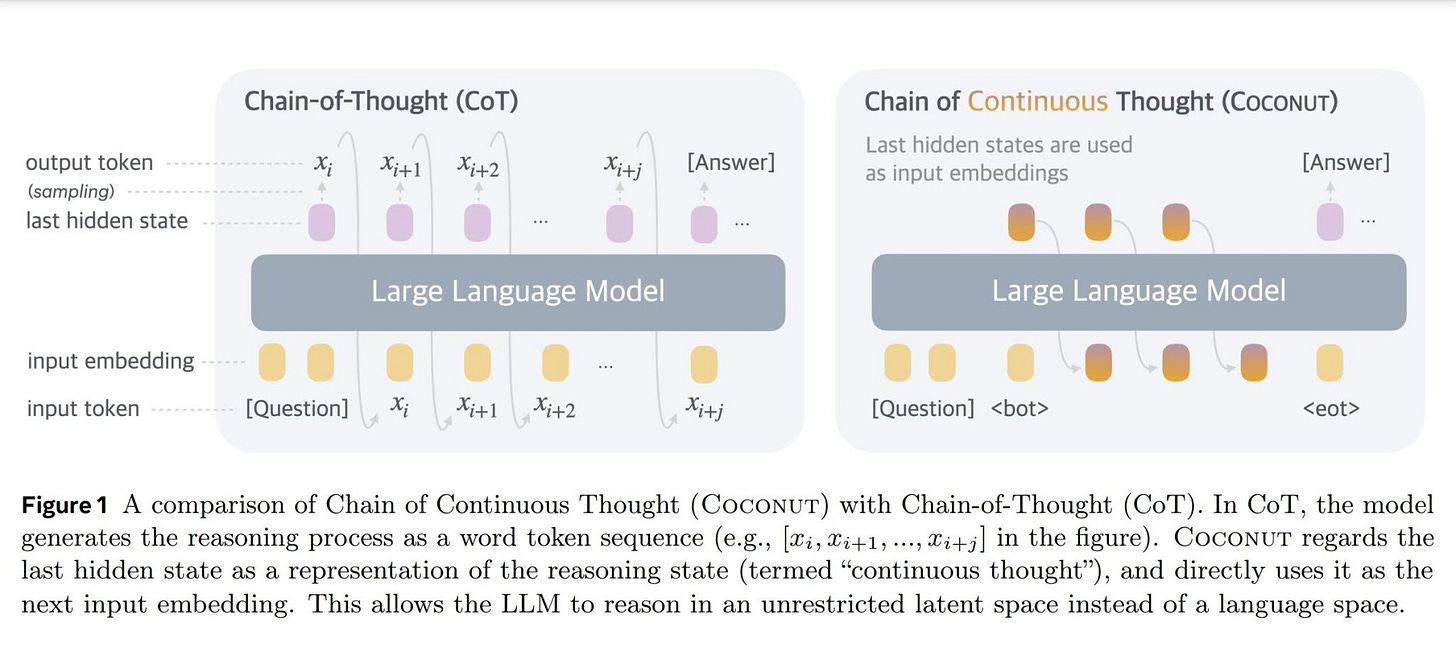
The first is the familiar token-level approach, where reasoning shows up as explicit intermediate steps. This is the land of Chain-of-Thought, Tree-of-Thoughts, and methods like CoConut that encourage compositional step-by-step breakdowns. The model literally “thinks out loud,” leaving a visible trail of tokens that looks like a student working through a math problem in their notebook.
It’s wonderfully interpretable; you can see exactly how the model reached its answer, debug errors, and align its outputs with how humans reason. But it’s also inefficient: generating all those extra steps takes time and compute, requires vast amounts of supervised data, and often risks degenerating into reasoning by memorization rather than genuine generalization.
We’ve discussed this in earlier pieces: CoT feels less like deep reasoning and more like externalized scratch work, which you can find here:
Latent-level reasoning
The second style hides reasoning inside the latent space. Models like Continuous Thought Machines (CTMs), Large Concept Models, or RLVR in the RPT paper don’t produce visible “scratch notes” at all. Instead, they reorganize their hidden representations to perform reasoning silently.
Think of it like a chess master visualizing moves in their head before committing to one. Nothing appears on paper, but the internal process is richer, faster, and often more scalable. This kind of reasoning doesn’t depend on generating token-by-token explanations, but instead leverages architectural changes that allow the model to carry out multi-step thought internally.
The trade-off, of course, is opacity. These models may reason better in practice, but we lose interpretability, as it’s much harder to peek into the hidden states and verify whether the model is reasoning correctly or just finding clever shortcuts.
The tension
So we’re left with a split:
Token-level reasoning gives interpretability but is costly and sometimes shallow.
Latent-level reasoning gives power and scalability but is opaque and harder to align.
And in both cases, improvements usually come from brute force: larger models, bigger datasets, and more compute. That raises the big question: is there a way to design reasoning directly into the architecture itself, instead of relying on scale?
This tension sets the stage for Hierarchical Recurrent Memory (HRM): a proposal to weave reasoning into the fabric of the model, not as output decoration or hidden trick, but as a core architectural loop.
The Ideal Case
So far, we’ve seen the two ends of the reasoning spectrum:
Token-level → interpretable, but slow and bloated.
Latent-level → efficient, but opaque and harder to control.
Neither feels quite right. Ideally, reasoning should look more like how humans approach hard problems:
For an easy puzzle, we may jump to the solution directly.
For a harder one, we pause, reflect, and let our thoughts run longer, sometimes looping until a satisfying structure emerges.
In other words, reasoning isn’t tied to how we speak, but to how we think.
That’s what some recent works like CTMs have hinted at thought steps can be internal, dynamic, and scaled with problem difficulty (in terms of ticks/time tokens). But even they face limits: interpretation is tricky, and architectures often feel patched onto existing LLM designs.
What Would the Ideal Case Look Like?
If we imagine a “perfect” reasoning model, it wouldn’t just output answers it would think like we do. Reasoning would be part of the model’s internal process, not something we infer from the tokens it produces.
Reasoning as part of the thought process
Instead of relying on explicit Chain-of-Thought steps, the model would carry out its reasoning internally. For example, when solving a complex combinatorics problem, the model wouldn’t generate every small calculation token by token. It would internally explore possibilities, evaluate constraints, and only output the final solution once it has converged on a coherent plan. Think of it as the difference between a student who mutters every step aloud versus one who silently solves the problem in their head and writes only the answer.
Dynamic computation time
The model should naturally spend more “thought steps” on harder problems and fewer on trivial ones. For instance, simple arithmetic like 7×8 would require almost no internal deliberation, whereas proving an algebraic identity or reasoning through a Sudoku puzzle would trigger longer internal reasoning loops. This dynamic time allocation makes the model both efficient and adaptive; like a chess player who spends 2 minutes on a quick endgame but 30 minutes on a tricky mid-game combination.
Unified architecture
Rather than patching reasoning modules onto a preexisting LLM, the architecture itself should make multi-step reasoning the default. All modules : memory, planning, and output would be integrated. Imagine a system where every forward pass inherently supports iterative refinement, much like the apprentice-manager duo: local exploration produces candidate solutions, which are then merged by a global planner before generating output. There’s no need for external tricks, heuristics, or post-hoc reasoning steps.
Smaller but sharper
We shouldn’t need billions of parameters to reason effectively. The ideal model would be small, efficient, but capable of picking up subtle relations quickly. For example, it could recognize that in a logic puzzle, the presence of a constraint like “A cannot sit next to B” immediately eliminates multiple possibilities without exhaustively enumerating every arrangement. Efficiency comes from structured thinking, not sheer scale.
Extendable to structural thinking
Finally, the architecture should be flexible enough to learn deeper, systematic reasoning. By training on structured datasets like OmniMath, it could move beyond causal reasoning to handle formal, mathematical-style abstractions. For example, the model could infer properties of new algebraic structures or systematically explore combinatorial spaces; reasoning not just step by step, but structurally, with rules and patterns generalized from experience.
In short, the ideal reasoning model is thoughtful, adaptive, integrated, efficient, and extendable which is a system designed to reason as naturally as a human mind, but with the precision and speed of a machine. And this is precisely where HRM is positioned. It doesn’t present itself as “a model that beats X benchmark,” but as a new architectural rhythm for reasoning fast local updates paired with slower, guiding oversight. Almost like importing the brain’s dual tempos directly into LLM design.
Methodology : how HRM actually works?
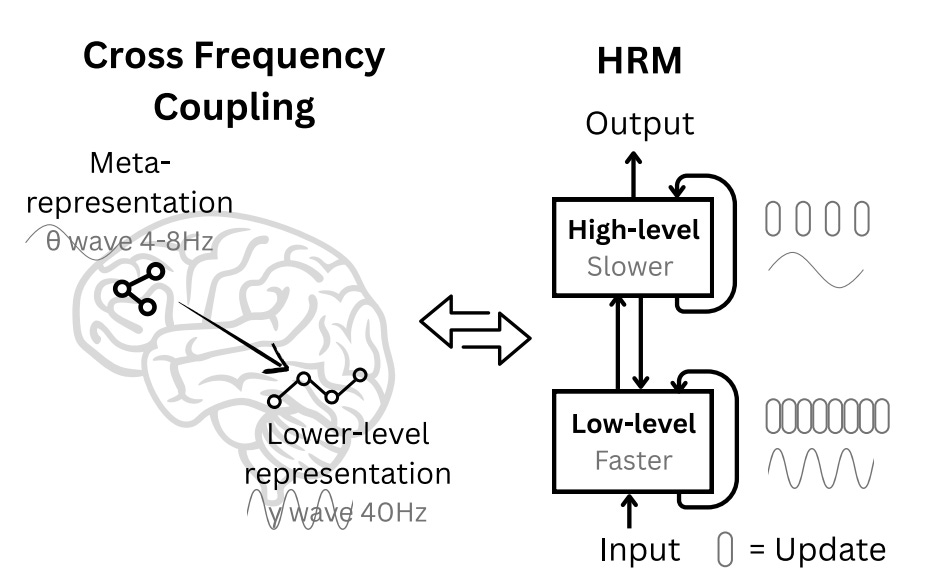
The core of HRM architecture are two sub-modules.
L-module : A continuously occurring shared parameter recurrent network
H-module : A interleaved/separated by K-steps module, that uses information aggregated by L-Module and combines it with previous steps and its own learning/representations.
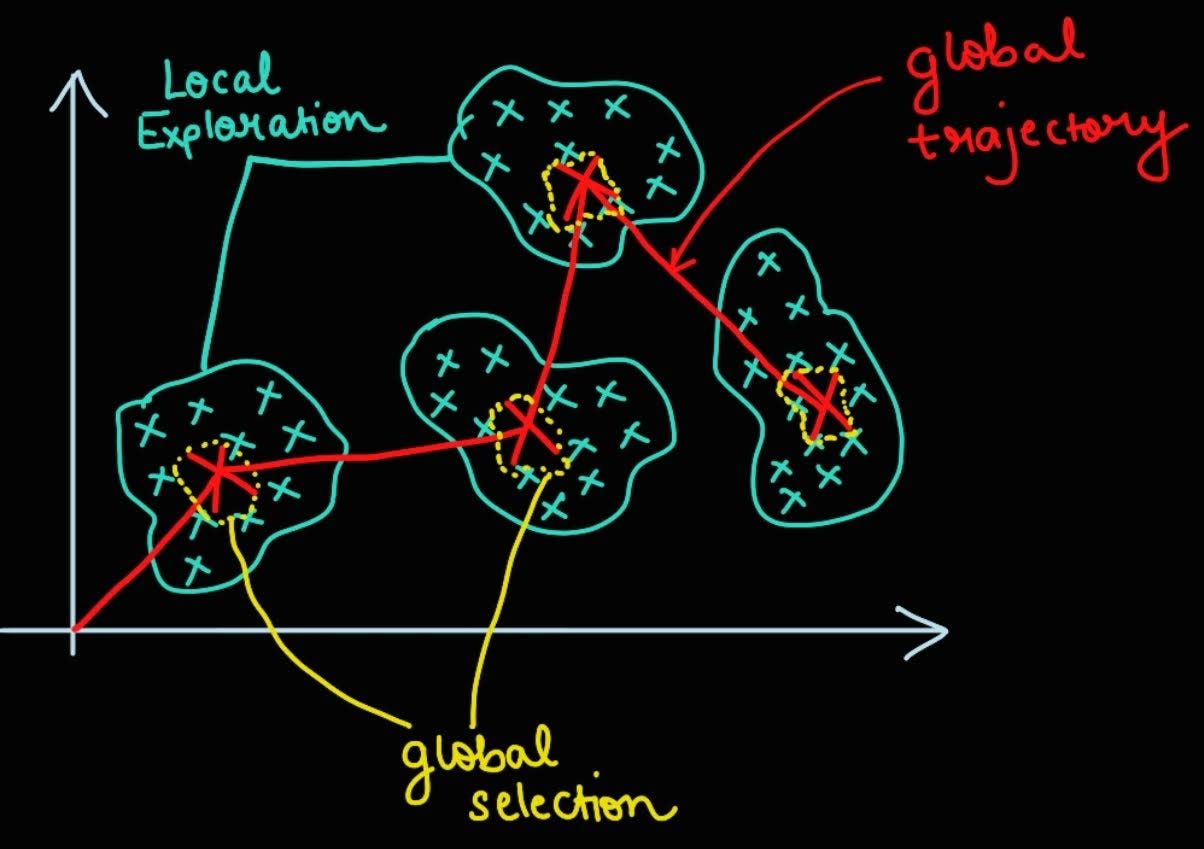
Let’s start with some intuition first to understand each module. Imagine a small team searching for a lost artifact in a big, cluttered warehouse.
The L-module is the quick apprentice: energetic, nimble, and impatient. They dart into nearby aisles, try handfuls of drawers, test many tiny hypotheses, and come back with a stack of “maybe-this” finds. They’re excellent at local exploration hence are fast, noisy, and massively parallel in the small neighborhoods they inspect.
The H-module is the experienced manager: slower, reflective, and conservative. They don’t rummage, instead they listen to the apprentice’s reports, compare the best candidates against broader context, filter out dead ends, and then update the search plan for the apprentice. This is global exploration / consolidation: merging local discoveries into a cleaner, higher-level belief about where the artifact must be.
How the loop/search works:
Apprentice runs a short sprint across nearby options, returns with a shortlist (many false positives).
Manager inspects the shortlist, discards noise, recognizes patterns (e.g., “all good leads cluster near the east wall”), and issues a new constraint or hint.
Apprentice restarts with the manager’s updated hint, the next sprint is faster and higher-yield because the search is now focused.
Repeat until the manager is confident enough to stop.
Why this matters (why HRM style helps):
Efficiency: many cheap local probes (L) + intermittent, smart aggregation (H) gives much deeper effective search without needing huge brute force or huge models.
Adaptivity: the manager can tell the apprentice to “think longer” on tough problems or “skip” easy ones, i.e., dynamic compute per example.
Robustness: local searches find diverse modes; the global step prevents the model from getting stuck in any single, low-value attractor by merging multiple local wins into a coherent plan.
Local vs global is also a filtering process, not just a frequency difference: the manager’s job is to select the best local fragments and fuse them into a tighter hypothesis (think: voting + pruning + generalization). That fused hypothesis then becomes the new context for the apprentice’s next local search. In that sense, HRM is less about “two clocks” and more about many fast scouts + one slow synthesizer.
(Conceptually similar to ideas in Google’s recent “Titans” work, which also separates short-term processing from a learned long-term memory/aggregation module that filters and preserves useful patterns at test time).
Short closing line you can drop into the Methodology intro:
HRM thinks like a scout-and-scribe duo, which is a combination of rapid, local experiments followed by careful global synthesis which gives small models a big, adaptive thinking depth without blowing up memory or training instability.
Architecture breakdown
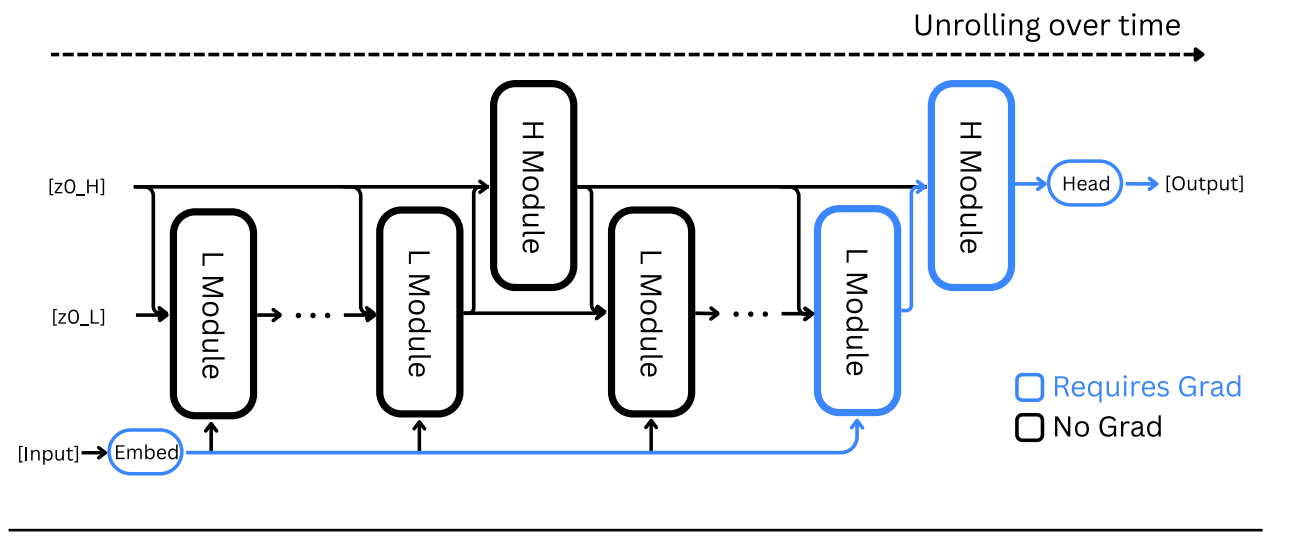
HRM has four learnable components (notation follows the paper):
Input network
f_I(⋅;θI): projects raw input x into a working representation x̃.Low-level recurrent module
f_L(⋅;θL): the fast inner loop; it updates every low-level timestep and is responsible for detailed search/refinement.High-level recurrent module
f_H(⋅;θH): the slow planner; it updates once per high-level cycle and conditions subsequent L cycles.Output network
f_O(⋅;θO): reads the H state after the final cycle and produces ŷ.
Dynamics : the forward pass unfolds over N high-level cycles each with T low-level timesteps (total steps i=1,…,NT).
Low module update (every timestep):
\(z^i_L = f_L\big(z^{i-1}_L,\; z^{i-1}_H,\; \tilde x;\; \theta_L\big)\)High module update (only when i%T == 0), at every T steps:
\(z_H^i = \begin{cases} f_H \big( z_H^{i-1}, z_L^{i-1}, \theta_H \big) & \text{if } i \equiv 0 \pmod{T} \\[2mm] z_H^{i-1} & \text{otherwise.} \end{cases} \)
Final prediction after N cycles:
(These equations are the core HRM recurrence; see the paper for the same symbols and a short PyTorch-style pseudocode snippet below.)
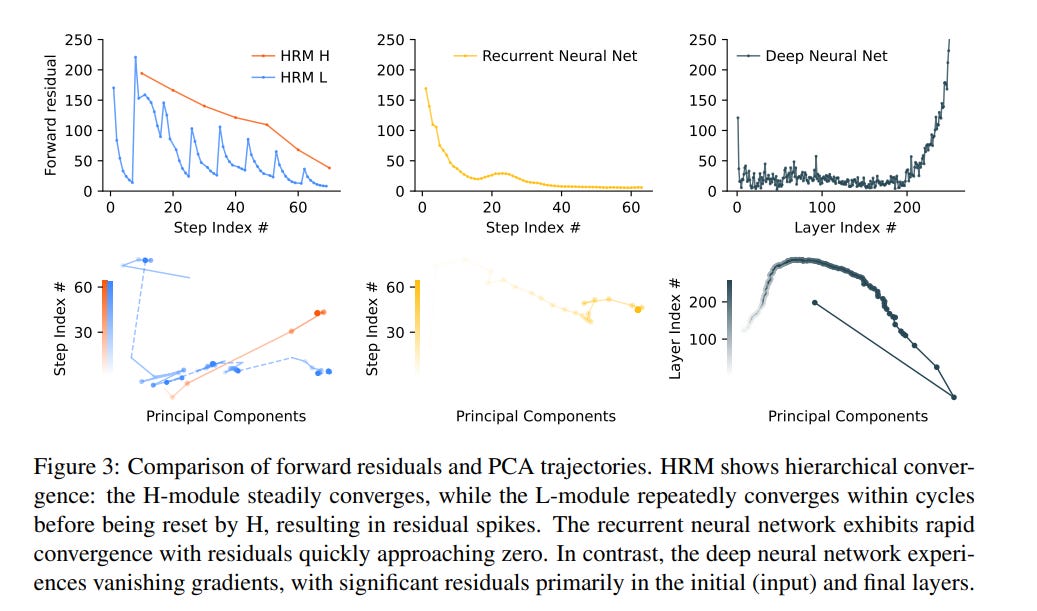
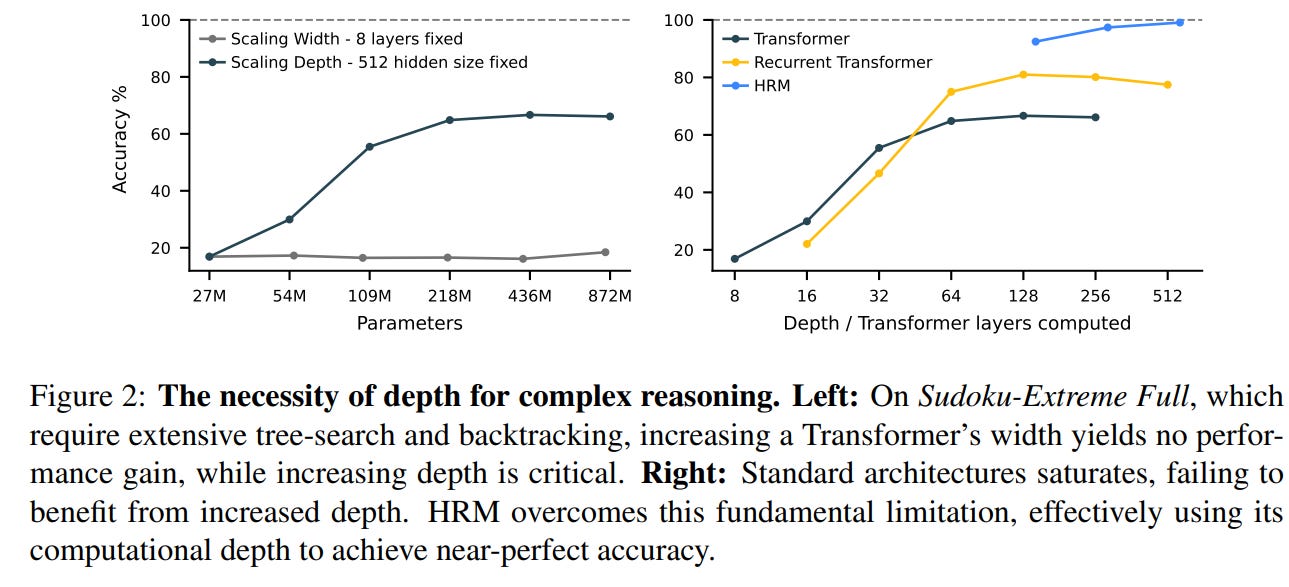
Why this avoids premature convergence?
A vanilla RNN tends to converge quickly to a fixed point and stall (updates vanish). HRM purposely lets the L-module converge locally within a cycle (so it finds a local equilibrium), then the H-module reads that final z_L, updates, and thus re-sets L’s context so L performs a new convergence to a different local equilibrium. The result is many distinct, nested computations (fast searches inside L guided by slow H updates), hence effective depth N×T without unstable training.
Training : constant memory, DEQ-style math, and deep supervision
One-step gradient approximation (O(1) memory).
Instead of running full BPTT through all NT timesteps (which costs O(T) memory), HRM uses a one-step gradient approximation grounded in Deep Equilibrium Model (DEQ) math and the Implicit Function Theorem. Intuitively: if the L-module reaches a (local) fixed point during its inner loop, you can compute gradients using the fixed point only, avoiding unrolling the whole trajectory. Practically HRM approximates the implicit Jacobian inverse with the first term of the Neumann series (i.e., treat (I−JF)^−1 ≈ I), yielding a stable and cheap gradient update path (output head → H final state → L final state → input embedding). This is the key to constant-memory training, which is really important.
Deep supervision (segment-wise updates).
HRM runs a sequence of segments (multiple forward passes). For a dataset sample (x,y), it computes a segment output (z^m, y^m) = HRM(z^(m−1), x; θ), computes segment loss L^m=Loss(y^m, y), updates parameters (optimizer step), then detaches the segment hidden state before continuing. This detaching makes gradients local to each segment and implements a practical 1-step approximation of the true recursive gradient; giving frequent feedback to the H-module and acting as regularization. The paper gives simple pseudocode showing how this looks in PyTorch.
Hence, combine the one-step gradient approximation (DEQ intuition) with deep supervision to get stable, memory-efficient training that still benefits from long effective depth.
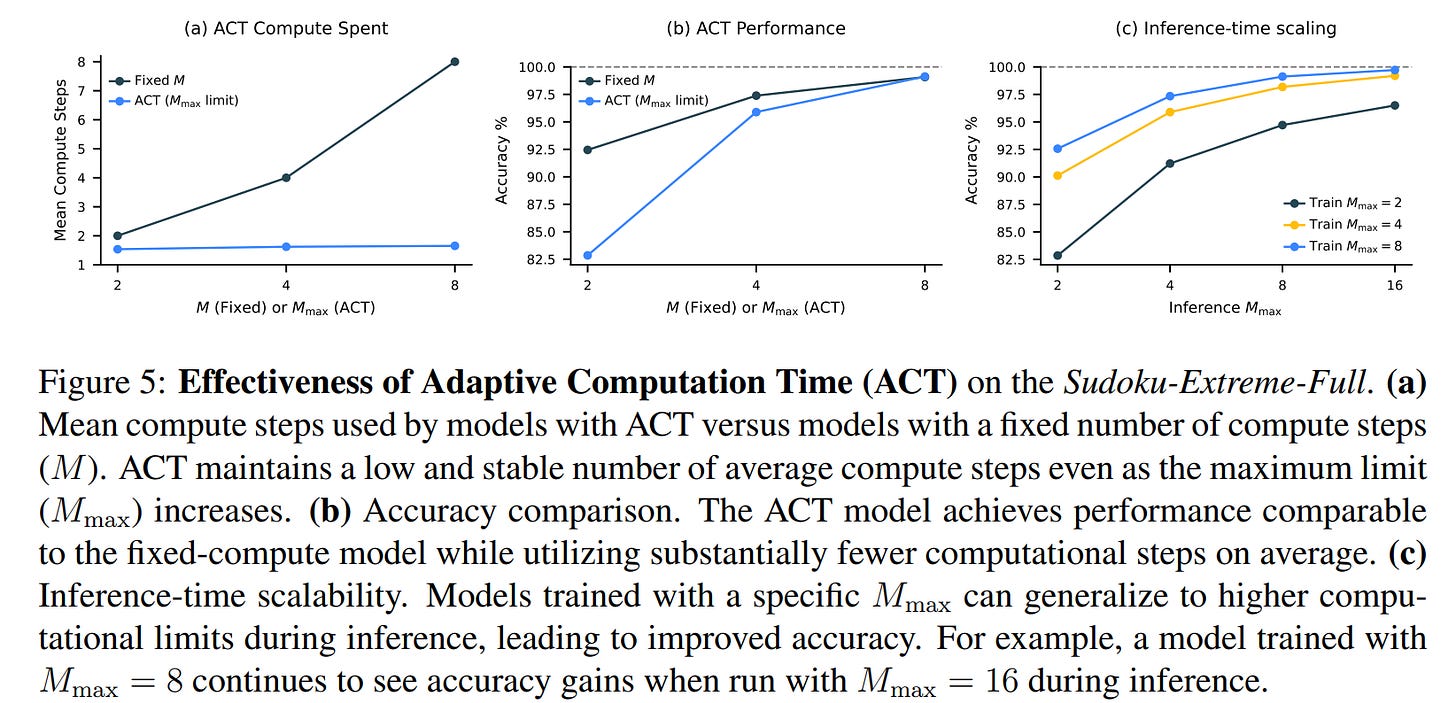
Halting / adaptive computation (ACT + Q-learning)
HRM uses an Adaptive Computational Time (ACT) style halting strategy to let the model “think longer” for hard examples and stop early for trivial ones. The implementation mixes ideas from ACT/PonderNet and a small Q-learning head:
At the end of each supervision segment mmm, a Q-head computes estimated Q-values for two actions : halt and continue (from the H-module’s final state):
\(\hat Q^m = \sigma(\theta_Q^\top z_H^{mNT})\)where σ is sigmoid (element-wise). The algorithm then chooses halt vs continue using a randomized strategy and constraints M_min,M_max (minimum/maximum segment counts).
Reward & targets (Q-learning): choosing “halt” ends the episode and gives a binary reward 1 if the current y^m equals the target y, else 0. Continue yields reward 0 and transitions to the next segment. The paper writes explicit Q-targets for both actions and trains the Q-head with a binary cross-entropy loss. The per-segment loss becomes:
\(L_{ACT}^m=\mathrm{Loss}(\hat y^m, y) \;+\; \mathrm{BinaryCrossEntropy}(\hat Q^m, \widehat G^m)\)so the model simultaneously learns to predict correct outputs and learn nearly-optimal stopping decisions. This is how HRM allocates compute adaptively.
Practical knobs: the algorithm samples M_min stochastically with probability ε (to encourage exploration/longer thinking), and uses a fixed M_max as an upper budget. At inference you can raise M_max to allow more compute without retraining (inference-time scaling).
Losses, objectives, and what actually gets optimized
Sequence loss (supervised): standard cross-entropy / task loss computed on the segment outputs y^m.
Q-head loss: binary cross-entropy between predicted Q values and Q-learning targets (constructs described above).
Total (per-segment):
\(L^m_{\text{ACT}} = \mathrm{task\_loss} + \mathrm{BCE}(\hat Q^m,\widehat G^m)\)Training alternates forward passes, segment-wise loss computation, optimizer update, detach, repeat. This makes the whole pipeline cheap in memory and frequent in feedback to the H-module.
Inference pipeline
Input: a partially filled 9×9 Sudoku board encoded as tokens → input embedding x~=f_I(x).
Init: z^0_L, z^0_H zeroed or learned init.
Run cycles:
For each high cycle k=1…N : run L for T low-timesteps to let it converge to a local equilibrium z^*_{L} in that cycle (repeated inner updates).
Update H once with the L final state:
\(z_H \leftarrow f_H(z_H, z^*_L)\)Optionally check Q-head (or preconfigured M_max) to decide whether to halt.
Stop when halting triggers or when you reach M_max.
Output : y^=fO(zH).
(Numbers T,N,M_max vary by task; the paper shows HRM strongly benefits from increasing the computational budget on long-horizon tasks like Sudoku.)
Complexity & resource tradeoffs
Memory: HRM’s 1-step gradient + deep supervision yields O(1) memory relative to BPTT’s O(T) (practical win for GPU batch sizes).
Computation: effective depth is N×T and you can increase reasoning depth at inference by increasing M_max (inference-time scaling). That gives flexible compute/quality tradeoffs.
Annotated pseudo-code
The HRM training loop can be broken into three conceptual blocks: the forward pass, the one-step gradient trick, and the deep supervision loop. Let’s unpack them one by one.
1. Forward Pass with Two Modules
def hrm(z, x, N=2, T=2):
x = input_embedding(x)
zH, zL = zInput embedding: Raw input
x(like a token sequence or feature vector) is mapped into a dense representation the model can work with.State initialization: The model maintains two states:
zL: low-level state (fast worker, updated every step).zH: high-level state (slow planner, updated everyTsteps).
This mirrors the math formulation where each timestep updates zL, and zH only updates occasionally.
2. No-Gradient Inner Loop
with torch.no_grad():
for _i in range(N * T - 1):
zL = L_net(zL, zH, x)
if (_i + 1) % T == 0:
zH = H_net(zH, zL)Why
no_grad?Running many steps with autograd would explode memory. Instead, HRM treats these inner updates as an “approximate fixed-point iteration”, hence, we simulate state evolution cheaply, without building a computation graph.Low updates: At every step,
L_netrefines the fast local statezL.High updates: Every
Tsteps,H_netintegrates the low state into a more abstract global viewzH.
Think of it as an apprentice doing trial-and-error at high speed, with a manager stepping in periodically to realign direction.
3. One-Step Gradient Trick
zL = L_net(zL, zH, x)
zH = H_net(zH, zL)
return (zH, zL), output_head(zH)After the cheap no-grad loop, we do one final forward step with gradients enabled.
This gives us differentiable outputs (
zH,zL) without having to backpropagate through the entire long unrolled sequence.The prediction head (
output_head) maps the high-level statezHto logits for classification (or other outputs).
This “one-step grad” is the key trick: it lets HRM approximate deep reasoning without paying the full gradient cost.
4. Deep Supervision Training Loop
for x, y_true in train_dataloader:
z = z_init
for step in range(N_supervision):
z, y_hat = hrm(z, x)
loss = softmax_cross_entropy(y_hat, y_true)
zH, zL = z
zH, zL = zH.detach(), zL.detach()
z = (zH, zL)
loss.backward()
opt.step()
opt.zero_grad()Segmented training: Instead of backpropagating through a very long run, we break training into multiple supervision segments.
Iterative refinement: Each call to
hrmproduces a prediction (y_hat) and updated states. The model gets feedback at every segment, not just the very end.Detach step: Hidden states are detached so that gradients don’t leak across segments. This keeps memory manageable and avoids unstable gradients.
Optimization: Standard backprop, optimizer step, and reset of gradients.
This block essentially says: run HRM in chunks, supervise each chunk, and progressively sharpen the planner and worker roles.
Hence, Putting It Together
Low module = fast exploration.
High module = periodic consolidation.
One-step grad = efficient training shortcut.
Deep supervision = frequent learning signals.
In summary, HRM combines hierarchical multi-timescale recurrence, fixed-point gradient approximations (DEQ flavor), deep segment supervision, and a learned halting/Q head to give a small model large effective depth and adaptive compute. The design deliberately trades token-level transparency for internal depth and stability and the training recipe is built to make that depth practical.
How HRM relates to other recurrent improvements (xLSTM, hierarchical RNNs, DEQs)?
DEQ connection: HRM’s one-step gradient approximation is explicitly grounded in DEQ / implicit differentiation ideas (explicitly referenced in the paper). DEQs provide the mathematical basis for using fixed-point gradients instead of full unrolling.
xLSTM and modern recurrent work: xLSTM extends LSTM with new gating/memory structures and residual block stacking to recover performance and scalability for recurrent designs. Like xLSTM, HRM is a modern push to make recurrence competitive again, but HRM’s emphasis is hierarchical multi-timescale cycles plus adaptive halting, rather than memory-structure and gating tweaks. So the relation is: both revive recurrence for large tasks, but they focus on different levers.
Hierarchical multiscale RNNs: HRM is conceptually close to earlier hierarchical/multiscale recurrent architectures (e.g., HM-RNNs) that use different update frequencies across modules; HRM’s novelty is the particular coupling, the hierarchical-convergence dynamic, the DEQ-style training approximation, and the RL-style halting head.
Results/Outcomes
Let us finally dive into the most important part, after such a long and complicated discussion, what did HRMs even achieved, with all of its special architecture, training and objectives.
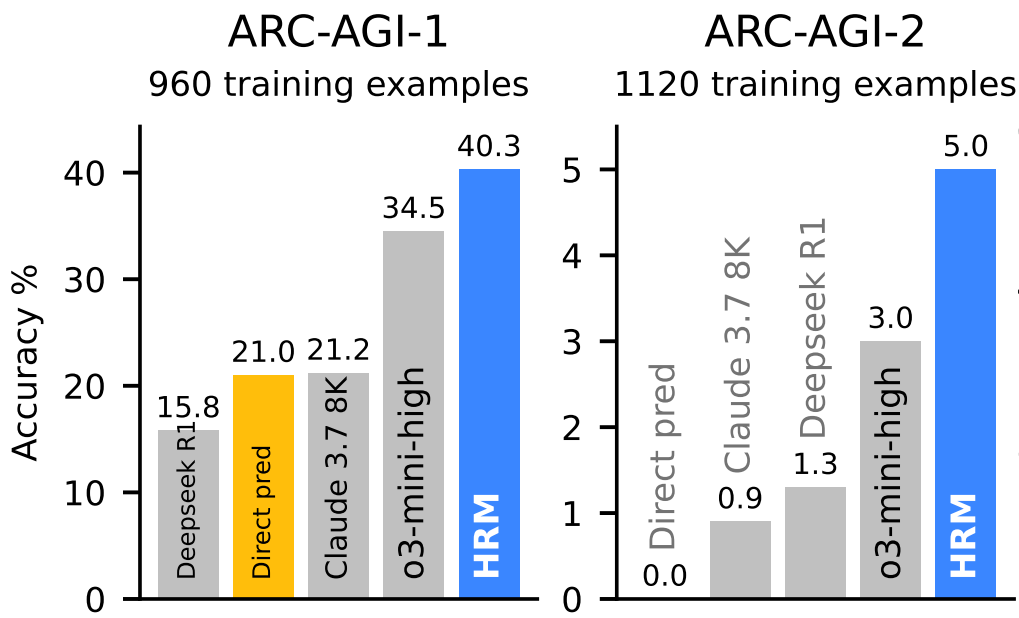
ARC-AGI (Abstract Reasoning, Key AGI Test)
HRM (27 M parameters, ~1,000 examples) achieves 40.3% accuracy on ARC-AGI-1, dramatically outperforming:
o3-mini-high (CoT-based): 34.5%
Claude 3.7 8K: 21.2%
Direct-prediction Transformer (same size): ~15.8%
On the tougher ARC-AGI-2, HRM scores about 5.0%, beating:
o3-mini-high: ~3.0%
Claude 3.7: ~0.9%
Why it matters: These are inductive reasoning puzzles intentionally designed to test abstraction and generalization with minimal context—visual, rule-based challenges. HRM not only surpasses direct competitors but does so with a fraction of the model size and data.
Sudoku-Extreme (9×9 Hard Puzzles)
HRM achieves near-perfect or 100% accuracy on extremely challenging Sudoku instances — puzzles that involve deep backtracking and search. Competitor models — whether same-size Transformers or CoT-based giants — consistently fail, often scoring 0%
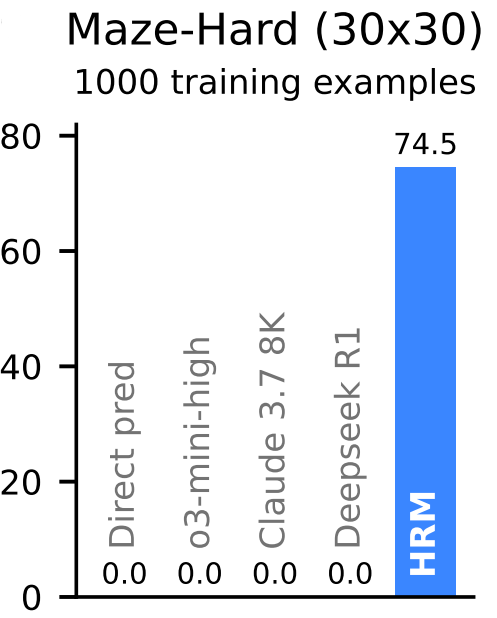
Maze-Hard (30×30 Pathfinding)
HRM again hits nearly perfect or 100% accuracy, reliably solving complex maze navigation tasks through iterative, structured latent planning. Baseline models remain at 0% accuracy, failing to find optimal paths
Efficiency & Data Use
No pretraining or CoT prompts: HRM is trained from scratch with only 1,000 examples per task.
Small model, big impact: Achieving better performance than many multilayered, pretrained LLMs using only 27 million parameters
Memory & compute efficient: Thanks to deep supervision and the one-step gradient trick, HRM trains with constant memory use, avoiding costly backpropagation-through-time
Thoughts
Here’s where things get interesting. HRMs are not just another “let’s throw more layers and parameters” approach. They represent a shift in architectural philosophy; away from flattening everything into token-by-token prediction and toward structured, time-aware reasoning loops.
But as with any architectural leap, a few reflections are worth unpacking:
1. The Bigger Trend: Dynamic Reasoning Architectures
We’ve seen a lot of movement lately in this space: CTMs introduce latent thought chains, RLVR in RPT treats reasoning as reward-optimized trajectories, and concept models cluster knowledge into semantically rich latent spaces. HRMs add themselves to this lineage; not as an isolated hack, but as part of a growing intuition:
Reasoning needs more than autoregression; it needs structure, recurrence, and time.
2. Where HRMs Shine vs Where They Struggle
Strengths:
Natural fit for problems requiring stepwise unfolding (math proofs, symbolic manipulation, logic puzzles).
Ability to halt dynamically like humans spending more thought on hard problems and skipping quickly over easy ones.
Architecture borrows from xLSTM-like recurrence, so it’s already compatible with stable optimization methods.
Limitations:
Interpretability takes a hit. The more we tuck reasoning into latent recurrences, the harder it is to “peek” at the thought process.
Scalability could be an issue as dynamic halting means variable compute per query, which complicates deployment at scale (cloud costs, inference predictability).
The experimental setup, while impressive, feels tuned to reasoning-heavy benchmarks. Open question: would HRMs still dominate in creative writing or multimodal tasks?
3. Subtle Concern: Are We Overfitting to Benchmarks?
A small but nagging thought: many of these reasoning architectures (CTMs, HRMs, etc.) show massive jumps on ARC-AGI, math-heavy datasets, or systematic reasoning tasks. But is that because the architecture is fundamentally superior, or because we’ve built a reasoning-shaped key for a reasoning-shaped lock?
In other words, what happens when the lock changes?
4. Looking Ahead
My personal hunch:
Hybrid models will emerge as token-level CoT for interpretability, latent HRM-style loops for depth. A two-track system.
Scaffolding datasets like OmniMath (systematic, compositional tasks) will be crucial in shaping these models toward general reasoning rather than “ARC-style puzzle solving.”
Another wild speculation is that maybe HRMs hint at a future where models don’t just generate sequences, but actually plan internal time budgets, like “I’ll think for 8 steps here because it’s tricky.” That’s… basically cognitive science creeping into deep learning.
In short: HRMs are a bold and necessary step. They won’t be the last word on reasoning, but they remind us that maybe the biggest breakthroughs won’t come from bigger transformers; but from architectures that learn how to think in time.
Conclusion
We began this journey by asking a simple but critical question: what would it take for language models to truly reason, not just recite?
Along the way, we explored how reasoning has traditionally been measured, from benchmarks like ARC-AGI to systematic tasks that stress compositionality and logic. We then looked at how modern LLMs attempt reasoning in two distinct ways : token-level methods like Chain-of-Thought, and latent-level approaches like Concept Token Models, each bringing unique strengths and weaknesses. From there, we imagined what the ideal reasoning system might look like: dynamic, integrated, efficient, and extendable, more like a thinker than a parrot.
This set the stage for HRM, an architecture that takes a significant step toward that ideal. We walked through its design: fast low-level updates for local exploration, slower high-level updates for global planning, and a clever one-step gradient trick that makes training feasible. With deep supervision ensuring steady progress, HRM shows how reasoning can be woven directly into the architecture rather than patched on. Then we dove into a quick tour at code level for understanding exact process step-by-step.
If there’s one takeaway, it’s this: HRM is not just another reasoning hack, but a pointer to what reasoning-first architectures could look like. It’s still early days challenges remain in scalability, generalization, and interpretability; but the direction is clear. We’re moving toward models that don’t just generate answers, but think their way to them both across space and time; in output and latent space.
You can finds the HRM paper here : https://arxiv.org/abs/2506.21734
CTM article : https://vizuara.substack.com/p/continuous-thought-machine-think
Benchmark article : https://vizuara.substack.com/p/a-primer-on-nlp-benchmarks